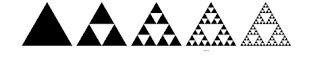We continue our discussion on inverse modeling to represent the system. An inverse model is a mathematical model that fits experimental data. It aims to provide a best fit to the data.
There are two ways by which we can select the appropriate model. The first is by observing trend lines which correspond to some well known mathematical formula. The second is on the observation of underlying physical processes which contribute towards the system. These physical interpretations contribute to model parameters.
In order to fit the data points, a model may use least squares of errors. the errors called residuals may be both positive or negative which result in inaccurate measure. Instead the squares of the errors can be minimized to give a better fit.
We used the least squares error minimization to fit the data points. Another way to do this is using Maximum likelihood estimation. The maximum likelihood estimation attempts to resolve this concern by asking "Given my set of model parameters, what is the probability that this data set occurred ?" This translates as likelihood for the parameters given the data.
The maximum likelihood estimation and the least squares error are related. For a Gaussian distribution, it is easy to see that the probability of the data set coming from the model parameters involves minimizing the negative natural log of probability which is the chi-square function of weighted residuals.
Minimizing Chi Square requires that we evaluate the model based on the parameters. One way to do this is to find where the derivatives with regard to the parameters are zero. This results in a general set of non-linear equations. The derivatives can be computed deterministically otherwise they can be approximated numerically using finite differences.
#codingexercise
Yesterday's problem on Sierpinski triangles can also be viewed to progress by a different pattern. The result of each step becomes one of the three subpatterns in the next triangle. Consequently, we can rewrite the method to count the number of triangles after each step as:
There are two ways by which we can select the appropriate model. The first is by observing trend lines which correspond to some well known mathematical formula. The second is on the observation of underlying physical processes which contribute towards the system. These physical interpretations contribute to model parameters.
In order to fit the data points, a model may use least squares of errors. the errors called residuals may be both positive or negative which result in inaccurate measure. Instead the squares of the errors can be minimized to give a better fit.
We used the least squares error minimization to fit the data points. Another way to do this is using Maximum likelihood estimation. The maximum likelihood estimation attempts to resolve this concern by asking "Given my set of model parameters, what is the probability that this data set occurred ?" This translates as likelihood for the parameters given the data.
The maximum likelihood estimation and the least squares error are related. For a Gaussian distribution, it is easy to see that the probability of the data set coming from the model parameters involves minimizing the negative natural log of probability which is the chi-square function of weighted residuals.
Minimizing Chi Square requires that we evaluate the model based on the parameters. One way to do this is to find where the derivatives with regard to the parameters are zero. This results in a general set of non-linear equations. The derivatives can be computed deterministically otherwise they can be approximated numerically using finite differences.
#codingexercise
Yesterday's problem on Sierpinski triangles can also be viewed to progress by a different pattern. The result of each step becomes one of the three subpatterns in the next triangle. Consequently, we can rewrite the method to count the number of triangles after each step as:
double GetCountRepeated(int n)
{
double result = 1;
For (int i = 0; i < n; i++)
{
result = 3 * result + 1 + 1;
}
Return result;
}