We were discussing Sierpinksi triangles earlier. An equilateral white triangle gets split into four equilateral sub-triangles and the one at the center gets colored red. This process is repeated for all available white squares in each iteration. You are given an integer m for the number of lines following and an integer n in each line following that for the number of iterations for each of which we want an answer.
We said the recursive solution is as follows:
static double GetRecursive(int n)
{
if (n == 0) return 1;
return GetRecursive(n-1) + GetRecursive(n-1) + GetRecursive(n-1)
+ 1 // for the different colored sub-triangle
+ 1; // for the starting triangle
}
The same problem can be visualized as one where the previous step triangle becomes one of the three sub-triangles in the next step.
In this case, we have
double GetCountRepeated(int n)
{
double result = 1;
for (int i = 0; i < n; i++)
{
result = 3 * result
+ 1 // for inner triangle
+ 1; // for outer triangle
}
return result;
}
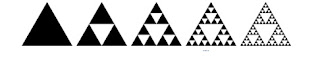
No comments:
Post a Comment